最近在读吴军老师的《计算之魂》，这是我读过唯一一本没有代码参考的算法书，也许以后会专门出一本《代码之魂》吧。

书中1.3 怎样寻找最好的算法，列举了使用不同方法求一个数列总和最大区间的不同算法，使得时间复杂度从O(N^3)降到O(N)，书中的序列如下

1.5, -12.3, 3.2, -5.5, 23.2, 3.2, -1.4, -12.2, 34.2, 5.4, -7.8, 1.1, -4.9

正确答案是：23.2, 3.2, -1.4, -12.2, 34.2, 5.4

1. 三重循环(O(N^3))

最直接粗暴的方法是利用三重循环，将所有序列一一组合，得到总和最大的区间，按照书中的思路，java代码的实现如下：

double[] a = {1.5, -12.3, 3.2, -5.5, 23.2, 3.2, -1.4, -12.2, 34.2, 5.4, -7.8, 1.1, -4.9};
int n = a.length;
double max = Double.MIN_VALUE;
int start = 0;
int end = 0;
for (int i = 0; i < n; i++) {
    for (int j = i; j < n; j++) {
        double sum = 0;
        for (int k = i; k <= j; k++) {
            sum += a[k];
        }
        if (sum > max) {
            max = sum;
            start = i;
            end = j;
        }
    }
}

System.out.println("Start: " + start);
System.out.println("End: " + end);

2. 基于方法1的优化

方法2可以去掉一层循环，是时间复杂度变为O(N^2)

double[] a = {1.5, -12.3, 3.2, -5.5, 23.2, 3.2, -1.4, -12.2, 34.2, 5.4, -7.8, 1.1, -4.9};
int n = a.length;
double max = Double.MIN_VALUE;
int start = 0;
int end = 0;
for (int i = 0; i < n; i++) {
    double sum = 0;
    for (int j = i; j < n; j++) {
        sum += a[j];
        if (sum > max) {
            max = sum;
            start = i;
            end = j;
        }
    }
}

System.out.println("Start: " + start);
System.out.println("End: " + end);

两段代码的比较如下图：

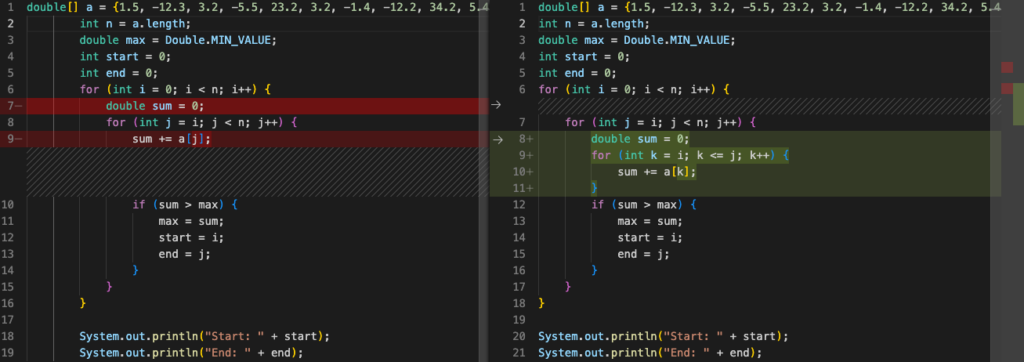
第三重循环的sum完全可以使用第二重循环序列的和相加，而不需要再循环一次，浪费计算资源。

书中描述：求p,q之间的总和S，S=(p,q)，如果想要得到S=(p,q+1)的和，只需要在原来的基础上再做一次加法即可。

方法二如果数组a为好几万个数字的组合，那么计算量是十几亿，但比方法一节约了上万倍的计算量。

3. 使用分治算法

将序列一分为二，分成从1到N/2和N/2+1到N，然后分别求它们的总和最大区间。代码如下：

double[] a = {1.5, -12.3, 3.2, -5.5, 23.2, 3.2, -1.4, -12.2, 34.2, 5.4, -7.8, 1.1, -4.9};
        int n = a.length;

        int[] start = {0};
        int[] end = {0};
        double max = maxSum(a, 0, n - 1, start, end);

        System.out.println("Start: " + start[0]);
        System.out.println("End: " + end[0]);
        System.out.println("Max sum: " + max);
        System.out.println("Max sum subarray: " + Arrays.toString(Arrays.copyOfRange(a, start[0], end[0] + 1)));
    }

    static double maxSum(double[] a, int l, int r, int[] start, int[] end) {
        if (l == r) {
            start[0] = end[0] = l;
            return a[l];
        }

        int mid = (l + r) / 2;
        int s1 = mid;
        double sum = 0;
        double max = Double.NEGATIVE_INFINITY;
        for (int i = mid; i >= l; i--) {
            sum += a[i];
            if (sum > max) {
                max = sum;
                s1 = i;
            }
        }
        sum = 0;
        int s2 = mid + 1;
        int e2 = mid + 1;
        for (int i = mid + 1; i <= r; i++) {
            sum += a[i];
            if (sum > max) {
                max = sum;
                e2 = i;
            }
        }

        double leftMax = maxSum(a, l, mid, start, end);
        double rightMax = maxSum(a, mid + 1, r, start, end);

        if (leftMax > max) {
            max = leftMax;
        }
        if (rightMax > max) {
            max = rightMax;
            start[0] = s2;
            end[0] = e2;
        }

        start[0] = s1;
        end[0] = e2;
        return max;
    }